Archive for the ‘Philosophy’ Category
About Intelligent Design
Tuesday, April 17th, 2012
Thermodynamics,
the Science of Heat, became an important science in the 19th century
when physicists started to improve the Steam-Machine. This blog is about
a recently discovered law of Thermodynamics called the Constructal Law.
The Constructal Law describes How Intelligent Systems emerge out of the Laws of Thermodynamics.
According to Thermodynamics our Universe moves from a highly improbable extreme hot state called the Big Bang to a highly probable extreme cold state called the Big Freeze.
The Big Bang was caused by a conflict between expanding and compressing (inflating) space in the Ocean of the Nothing (the Zero Point-Field) that contains infinite possibilities. This conflict generated a high level of turbulence.
Our Universe is one of the many bubbles that drift in the Sea. At a certain moment the Bubble will dissolve and space will become evenly distributed.
To reach the Big Freeze in finite time every new state of our Universe has to be more probable than the old state. The Probability of a System is called Entropy in Thermodynamics.
Energy always moves from High (Chaos) to Low (Order) Temperature. This is the main reason why most of the energy of Earth comes from our Sun.
With help of the Electro-Magnetic radiation of the Sun we call Light, plants, algae and bacteria transform simple molecules into complex organic structures (Biomass = Potential Chemical Energy) and store the energy of the Sun. Bacteria and Fungi brake up these structures, produce heat, reduce the complexity, and close the Cycle.
The Input of the Heat of the Sun has to be compensated by a comparable Output of Radiation otherwise Earth would be burned instantly. The difference between the Input and Output of Energy is transformed into Movements on Earth.
The Earth’s climate is a huge flow system. It circulates air and water from the tropics to the poles and back. These flows develop as air and water move from hot to cold regions, a result of variation in the heating of the Earth’s surface by the sun.
The Earth is not only heated by the Sun. The hot kernel of the Earth is surrounded by a small crust. At certain places on Earth and the Sea the rotating pool of the magma-ocean produces a lot of energy.
The Earth with its solar heat input, heat rejection, and wheels of atmospheric and oceanic circulation, is a heat engine without shaft. Its maximized mechanical power cannot be delivered, but is instead destined to dissipate through air and water friction and other forms of heat loss. It produces maximum power, which it then dissipates at a maximum rate.
The earth is wasting a lot of energy because the transmission of most of its energy is not contained in a Tube-like-system.
The system maximizes the sum of the work done driving the planetary circulation, and the heat rejected back to space at the cold end of the heat engine.
When the speed of the planetary circulation is low, so are the turbulent losses. As speed increases, up to a certain point the sum of work done (circulation speed) and heat rejected also increasing until the turbulence starts to interfere with the circulation and actually decrease the total of work done and heat rejected. That is the point, “the edge of turbulence”, at which the system will naturally run.
Every flow system tries to find the perfect balance between movement and friction.
The interesting point is that friction is movement in opposition to itself.
The biomass on Earth is direct or later (Oil, Gaz, Coal) consumed by all kinds of organisms. In Food-Webs Organisms are consumed by other organisms.
We, the Humans, describe the interaction of the organisms in the Food-Webs as a Struggle for Live, a Survival of the Fittest, but the flow of energy in the food webs could also be seen as an adaptive chain of chemical reactions that are performed in self-moving, self-reproducing chemical factories.
Energy is Potential Movement. The potential energy stored in the biomass on Earth is transformed into circular movement (kinetic energy). During this transformation Heat is produced. Heat is the waste produced by a restrained non-effective movement.
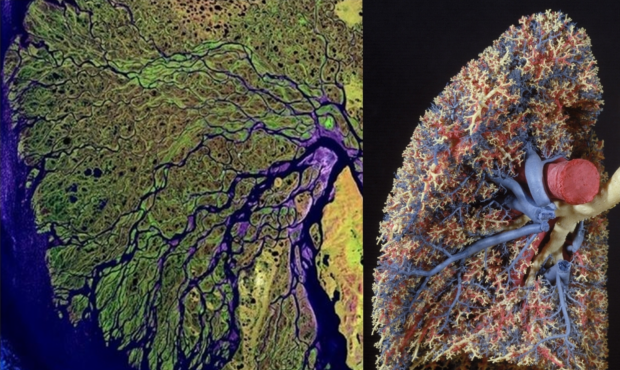
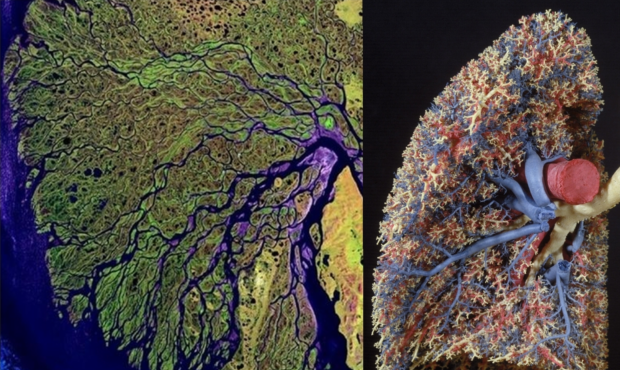
The energy of the Sun produces all kinds of movements on Earth. Examples are river-delta’s, our respiratory system and the weather-system.
According to Constructal Theory the generation of design (configuration, patterns, geometry, shape, structure, rhythm) in nature is a physical phenomenon that unites all animate and inanimate systems. Design in Nature always shows itself as systems that flow and improve themselves. Systems improve themselves because the movement from chaos to order takes many discrete steps.
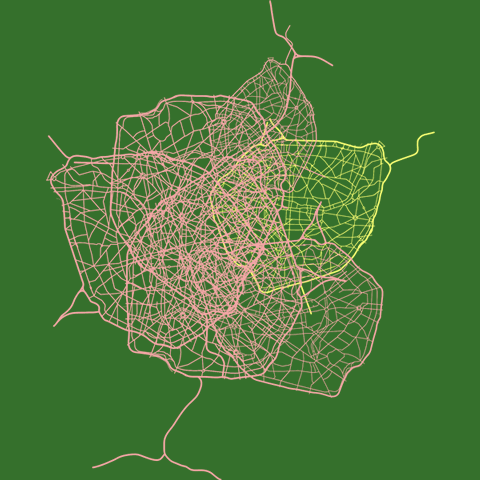
Biological organisms are flow systems. River basins are flow systems. A Tree is a flow system. The Traffic System is a flow system. The City of Paris is a flow system. The Financial Market is a flow system. The Internet is a flow system. A Proces-Manager is a flow system.
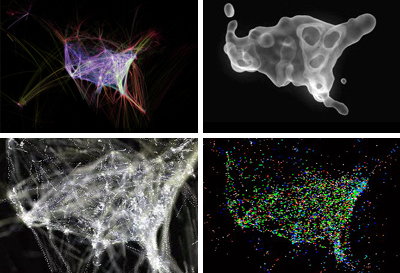 All these flow systems must be structured (architecturally designed)
in such a way that the currents that flow (Life Energy, Water, Air,
Electricity, Gaz, People, Cars, Trains, Airplanes, Content, Money)
increasingly get to where they need to go. This gives shape and
structure to everything that evolves over time.
All these flow systems must be structured (architecturally designed)
in such a way that the currents that flow (Life Energy, Water, Air,
Electricity, Gaz, People, Cars, Trains, Airplanes, Content, Money)
increasingly get to where they need to go. This gives shape and
structure to everything that evolves over time.
Flow Systems always remove the Resistance to the Flow themselves.
Constructal Law is formulated as follows: “For a finite-size system to persist in time (to live), it must evolve in such a way that it provides easier access to the imposed currents that flow through it.”.
Nature always provides Resistance to Change (Heat, Erosion, Friction) and this resistance is provided by the Systems of the Past. The current Order resists the potential Chaos of Free Moving Energy.
The Paths of Change of our Universe always move in the same way. The pattern looks like a Moebius Ring, the number 8, because this is the only way to cope with the polarity of the movements. In a Moebius Ring two Opposite Cyclic Movements are perfectly United.
A Moebius Ring is a 2D-structure that operates in 3D because it needs a Twist to operate.
According to Constructal Theory the Energy of the Sun creates two types of Systems called Engines and Brakes.
Engines are the most effective and efficient states in the evolution of our Universe. They have found the best way to cope with the resistance that is provided by the Brakes. Brakes are the old systems like trees, forests and natural or constructed dams that slow down the movement so the potential energy can be stored.
If the Energy of the Sun is not stored, the Self-Reproducing Systems are unable to evolve to a higher level of organization. If every Resistance would be gone the Flow-Systems would Flow in a Radial Pattern to every Direction possible.
If we remove the Natural Brakes (Forests, River-delta’s) the Expansive Flow-systems will take over control and the Smart Highly Improbable Next Generation Brake Systems, the Organisms would die.
We, the Humans, are here to Resist the Engines that give the Flow-Systems the opportunity to make Everything the Same. Every Thing has to become the Same because the Universe does not discriminate. Every configuration has the same chance to be alive.

Dependent on the type of flow there are standard solutions to the dualities that are provided by the eternal battle between engine (movement) and brake (not-movement).
 The standard solution can be calculated using the Laws of
Thermodynamics. Tree (or Leaf)-shaped fractal systems are for example
the best solution for a One-to-Many (or Many-to-One) Flow. The Flow Systems always converge to these Shapes.
The standard solution can be calculated using the Laws of
Thermodynamics. Tree (or Leaf)-shaped fractal systems are for example
the best solution for a One-to-Many (or Many-to-One) Flow. The Flow Systems always converge to these Shapes.
Our Earth is rotating, spinning and moving around our moving Sun. The influx of Energy on every area on Earth is changing all the time. This means that every Flow-System on Earth has to adapt to the short term and long term changing Energy Input of the Sun.
The stability of a Flow-System, the Resistance to Change, is highly dependent on the Resilience of the System.
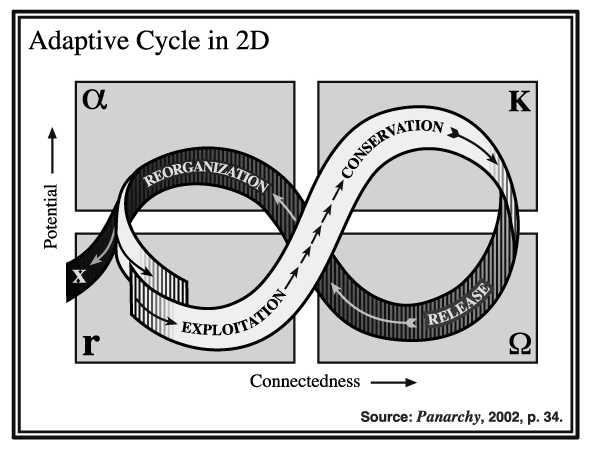
According to the theory of Panarchy the Resilience of a System is dependent on the Potential and the Connectedness of a System.


The Vacuum is the Eternal Flow System of Creation. It contains everything that is possible even the impossible, the Empty Set.
The Tao is the Channel of the Energy of Life. If Constructal Law is Right we have to give easier access to this Flow. We have to become the River to move to our final destination, the Sea of the Nothing.
LINKS
A video about Constructal Theory
About the Higgs Field and the Big Bang
About Innovation and Thermodynamics
About the Big Bang
About Friction
About the Constructal Theory of David Deutsch
The Website about Constructal Theory
An Introduction into Constructal Theory
About Morphology
About Panarchy
About Kleiber’s Law
About Genetic Similarity Theory
Why a City is an Organism
About the Triangle of Pascal and the Holy Trinity
About the Holy Trinity
About Constructal Law and the Trinity
Attraction + Obstacles = Excitement
About the Law of three & Gurdjieff
The Constructal Law describes How Intelligent Systems emerge out of the Laws of Thermodynamics.
According to Thermodynamics our Universe moves from a highly improbable extreme hot state called the Big Bang to a highly probable extreme cold state called the Big Freeze.
The Big Bang was caused by a conflict between expanding and compressing (inflating) space in the Ocean of the Nothing (the Zero Point-Field) that contains infinite possibilities. This conflict generated a high level of turbulence.
Our Universe is one of the many bubbles that drift in the Sea. At a certain moment the Bubble will dissolve and space will become evenly distributed.
To reach the Big Freeze in finite time every new state of our Universe has to be more probable than the old state. The Probability of a System is called Entropy in Thermodynamics.
Energy always moves from High (Chaos) to Low (Order) Temperature. This is the main reason why most of the energy of Earth comes from our Sun.
With help of the Electro-Magnetic radiation of the Sun we call Light, plants, algae and bacteria transform simple molecules into complex organic structures (Biomass = Potential Chemical Energy) and store the energy of the Sun. Bacteria and Fungi brake up these structures, produce heat, reduce the complexity, and close the Cycle.
The Input of the Heat of the Sun has to be compensated by a comparable Output of Radiation otherwise Earth would be burned instantly. The difference between the Input and Output of Energy is transformed into Movements on Earth.
The Earth’s climate is a huge flow system. It circulates air and water from the tropics to the poles and back. These flows develop as air and water move from hot to cold regions, a result of variation in the heating of the Earth’s surface by the sun.
The Earth is not only heated by the Sun. The hot kernel of the Earth is surrounded by a small crust. At certain places on Earth and the Sea the rotating pool of the magma-ocean produces a lot of energy.
The Earth with its solar heat input, heat rejection, and wheels of atmospheric and oceanic circulation, is a heat engine without shaft. Its maximized mechanical power cannot be delivered, but is instead destined to dissipate through air and water friction and other forms of heat loss. It produces maximum power, which it then dissipates at a maximum rate.
The earth is wasting a lot of energy because the transmission of most of its energy is not contained in a Tube-like-system.
The system maximizes the sum of the work done driving the planetary circulation, and the heat rejected back to space at the cold end of the heat engine.
When the speed of the planetary circulation is low, so are the turbulent losses. As speed increases, up to a certain point the sum of work done (circulation speed) and heat rejected also increasing until the turbulence starts to interfere with the circulation and actually decrease the total of work done and heat rejected. That is the point, “the edge of turbulence”, at which the system will naturally run.
Every flow system tries to find the perfect balance between movement and friction.
The interesting point is that friction is movement in opposition to itself.
The biomass on Earth is direct or later (Oil, Gaz, Coal) consumed by all kinds of organisms. In Food-Webs Organisms are consumed by other organisms.
We, the Humans, describe the interaction of the organisms in the Food-Webs as a Struggle for Live, a Survival of the Fittest, but the flow of energy in the food webs could also be seen as an adaptive chain of chemical reactions that are performed in self-moving, self-reproducing chemical factories.
Energy is Potential Movement. The potential energy stored in the biomass on Earth is transformed into circular movement (kinetic energy). During this transformation Heat is produced. Heat is the waste produced by a restrained non-effective movement.
The energy of the Sun produces all kinds of movements on Earth. Examples are river-delta’s, our respiratory system and the weather-system.
According to Constructal Theory the generation of design (configuration, patterns, geometry, shape, structure, rhythm) in nature is a physical phenomenon that unites all animate and inanimate systems. Design in Nature always shows itself as systems that flow and improve themselves. Systems improve themselves because the movement from chaos to order takes many discrete steps.
Biological organisms are flow systems. River basins are flow systems. A Tree is a flow system. The Traffic System is a flow system. The City of Paris is a flow system. The Financial Market is a flow system. The Internet is a flow system. A Proces-Manager is a flow system.

Flow Systems
Flow Systems always remove the Resistance to the Flow themselves.
Constructal Law is formulated as follows: “For a finite-size system to persist in time (to live), it must evolve in such a way that it provides easier access to the imposed currents that flow through it.”.
Nature always provides Resistance to Change (Heat, Erosion, Friction) and this resistance is provided by the Systems of the Past. The current Order resists the potential Chaos of Free Moving Energy.
The Paths of Change of our Universe always move in the same way. The pattern looks like a Moebius Ring, the number 8, because this is the only way to cope with the polarity of the movements. In a Moebius Ring two Opposite Cyclic Movements are perfectly United.
A Moebius Ring is a 2D-structure that operates in 3D because it needs a Twist to operate.
According to Constructal Theory the Energy of the Sun creates two types of Systems called Engines and Brakes.
Engines are the most effective and efficient states in the evolution of our Universe. They have found the best way to cope with the resistance that is provided by the Brakes. Brakes are the old systems like trees, forests and natural or constructed dams that slow down the movement so the potential energy can be stored.
If the Energy of the Sun is not stored, the Self-Reproducing Systems are unable to evolve to a higher level of organization. If every Resistance would be gone the Flow-Systems would Flow in a Radial Pattern to every Direction possible.
If we remove the Natural Brakes (Forests, River-delta’s) the Expansive Flow-systems will take over control and the Smart Highly Improbable Next Generation Brake Systems, the Organisms would die.
We, the Humans, are here to Resist the Engines that give the Flow-Systems the opportunity to make Everything the Same. Every Thing has to become the Same because the Universe does not discriminate. Every configuration has the same chance to be alive.

Dependent on the type of flow there are standard solutions to the dualities that are provided by the eternal battle between engine (movement) and brake (not-movement).

Paris is a Flow System
Our Earth is rotating, spinning and moving around our moving Sun. The influx of Energy on every area on Earth is changing all the time. This means that every Flow-System on Earth has to adapt to the short term and long term changing Energy Input of the Sun.
The stability of a Flow-System, the Resistance to Change, is highly dependent on the Resilience of the System.
According to the theory of Panarchy the Resilience of a System is dependent on the Potential and the Connectedness of a System.
In the Exploitation/Conservation phase of
the Adaptive Panarchy-Cycle the Constructal Engines become more
efficient (producing more Potential) and Connected. This means that the
amount of possible paths in the River-delta of the System is reduced.
This amount determinates the resilience of the system.
At the state of maximum production and
maximum connection (conservation) the system is spending all its
potential at self-reproduction and is highly vulnerable to external
disturbances. At a certain moment when a disturbance destroys the
majority of the paths the system collapses (release).

Revolt: A small Wildfire can destroy a complete Ecology
The bits and pieces, the components, of the
scattered ecology are reassembled sometimes in a different way
(reorganization) and the system starts again most of the time on a
higher level of organization.
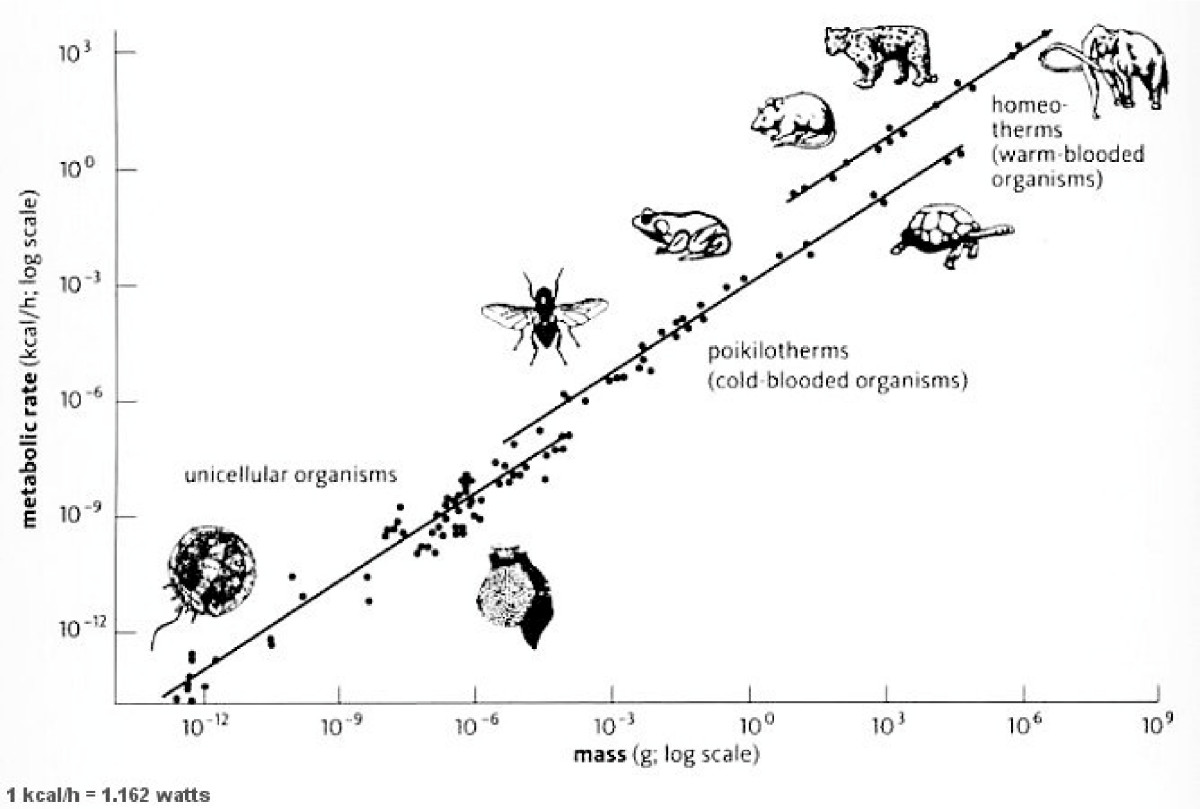
Kleiber’s Law is
an example of the Constructal Law. It shows the many levels of
organization that have occured since the chemical factories of the
bacteria started to work together. Kleiber’s Law can be extented to the
level of the Community and the City.

The Panarchy Cycle is Self-Similar. It
repeats itself on many Scales. The higher the scale the bigger the
impact and the slower change takes place.
The Scales are interconnected. A huge
disturbance on a lower scale (Revolt) can have an huge impact on a
higher scale when both cycles are moving into the Release State.
A Slow moving High Level Cycle can help to
restructure a fast moving cycle by providing the template of the way the
components were originally assembled (its CommunityDNA) (Remember).
Constructal Law is a Law of Thermodynamics. Thermodynamics has evolved into a Statistical Theory called Statistical Mechanics. To calculate a probability you have to define the Space of all Possibilities of a System, the Phase Space.
When you don’t know what a system will look
like it is impossible to calculate the Phase Space. To calculate the
possibilities of Constructal Law you have to imagine the possible
constructions of Mother Nature.
It is possible to play with Probability
Theory without knowing the exact Phase Space. In this case you have to
look at the probabilities of the probabilities. These probabilities are
described by the Triangle of Pascal.
Behind the Triangle of Pascal a new Triangular Structure shows itself.
This pattern goes on and on until the primary Triangle of Creation, the Holy Trinity, is reached.
The Trinity is a combination of Desire
(Mother, Female, Expansion, FLOW), Control (Father, Male, Compression,
BRAKE) and the combination of both Expansion AND Compression also called
the Void or the Tao. In Physics the Void is called the Vacuum or the Zero-Point-Field.
When we have moved back in time and have reached the state of the
Trinity we are very close to the Big Bang. The Big Bang is a result of
the Union of the Opposites (Yin/Yang, Male/Female, Matter/Anti-Matter, Expansion/Compression) that both came out of the Void.The Vacuum is the Eternal Flow System of Creation. It contains everything that is possible even the impossible, the Empty Set.
The Tao is like a well:
used but never used up.
It is like the eternal void:
filled with infinite possibilities.
It is hidden but always present.
I don’t know who gave birth to it.
It is older than God.
(Tao Te Ching 4)
According to Constructal Law every finite-size system must evolve in
such a way that it provides easier access to the imposed currents that
flow through it.The Tao is the Channel of the Energy of Life. If Constructal Law is Right we have to give easier access to this Flow. We have to become the River to move to our final destination, the Sea of the Nothing.
LINKS
A video about Constructal Theory
About the Higgs Field and the Big Bang
About Innovation and Thermodynamics
About the Big Bang
About Friction
About the Constructal Theory of David Deutsch
The Website about Constructal Theory
An Introduction into Constructal Theory
About Morphology
About Panarchy
About Kleiber’s Law
About Genetic Similarity Theory
Why a City is an Organism
About the Triangle of Pascal and the Holy Trinity
About the Holy Trinity
About Constructal Law and the Trinity
Attraction + Obstacles = Excitement
About the Law of three & Gurdjieff
About Perspective
Thursday, February 2nd, 2012
When we Look with our Eyes and not with our Mind we can See that
Space looks very different from what we Think it is. In Our Space
Parallel Lines meet at Infinity.
Around 1400 during the Renaissance Painters started to look at Space with their own Eyes and discovered the Rules of Perspective Drawing.
Between 1600-1800 Perspective Theory changed from a Theory of Art to a Theory of Mathematics called Projective Geometry.
It took 400 Years before a few Mathematicians realized that Projective Geometry was the Foundation of Mathematics and it took another 100 years before Projective Geometry started to influence Physics.
In 1908 Hermann Minkowski discovered that Einstein’s Theory of Special Relativity could be analysed using Projective Geometry. Minkowski created a 4D Space-Time Metric Geometry in which he added one Time Dimension.
Many experiments now show that 4D-Space-Time is not sufficient to incorporate what Time Really is.
The essence of Our Universe is Movement, Expanding Space, and Movement = Space/Time (Space Divided By Time).
Both Time and Space are 3-Dimensional and represent a Different, Reciprocal, Complementary (Dual), View on Movement.
We can move independently in Time OR Space and in Time AND Space (The Chronotope).
The Future is Expanding Space with Infinite Potential.
Time moves behind Space and Scales Space.
About Perspective Drawing
A Mathematical Theory of Perspective Drawing could only be developed when the Renaissance freed painters to depict Nature in a way closer to what they Observed.
In the Middle Ages Social Status was very important. Important People or Buildings were always emphasized.
In the Renaissance the Artists started to look with their own Eyes and Created Pictures where the Viewer looked through the Eyes of the Painter.
The Florentine architect Filippo Brunelleschi (1337-1446) studied Greek Geometry, developed a theory of perspective and undertook painting just to apply his geometry.
The first treatise, Della pittura (1435) by Leone Battista Alberti (1404-72) furnished most of the rules.
Alberti regarded mathematics as the common ground of Art and the Sciences. “To make clear my exposition in writing this brief commentary on painting,” Alberti began his treatise Della pittura, “I will take first from the mathematicians those things which my subject is concerned”.
Alberti stressed that “all steps of learning should be sought from nature“. The ultimate aim of an artist is to imitate nature.
 Alberti did not mean that artists should imitate nature objectively,
as it is, but the artist should be especially attentive to beauty, “for in painting beauty is as pleasing as it is necessary“.
Alberti did not mean that artists should imitate nature objectively,
as it is, but the artist should be especially attentive to beauty, “for in painting beauty is as pleasing as it is necessary“.
The work of art is according to Alberti so constructed that it is impossible to take anything away from it or add anything to it, without impairing the beauty of the whole.
Beauty was for Alberti “the harmony of all parts in relation to one another,” and subsequently “this concord is realized in a particular number, proportion, and arrangement demanded by harmony“.
Alberti’s thoughts on harmony were not new – they could be traced back to Pythagoras – but he set them in a fresh context, which well fit in with the contemporary Aesthetic Discourse.
One of the earliest Artists to produce a book on how to draw in perspective was Albrecht Dürer. As well as discussing geometric methods, he also illustrated his book with a set of woodcuts showing practical tools for accurate perspective drawing. Other Artists like Leonardo Da Vinci developed comparable tools.
About Projective Geometry
Projective Geometry formalizes one of the Central Principles of Perspective Drawing and of Human Perception: Parallel Lines Meet at Infinity.
 In Euclidean geometry, constructions are made with Ruler (Line) and Compass (Circle). Projective Geometry only require a Ruler.
In Euclidean geometry, constructions are made with Ruler (Line) and Compass (Circle). Projective Geometry only require a Ruler.
In Projective Geometry one Never Measures Any Thing, instead, one Relates one Set of Points to another by a Line.
Alberti was the first to ask what two pictures have in common if two drawing screens are interposed between the viewer and the object, and the object is projected onto both resulting in two different pictures of the same scene.
The basic idea behind Linear Perspective is simple: in every painting an artist creates a “floor” or area of the painting where the figures and/or objects will be placed. The floor ends at a horizon line, and the horizon line has a Vanishing Point or Point of Convergence on it.
The artist then draws parallel lines radiating from the vanishing point outward. Images closest to the vanishing point should appear smaller and closer together, and images farthest from the vanishing point should appear larger and farther apart, giving the impression of depth and space in the painting.
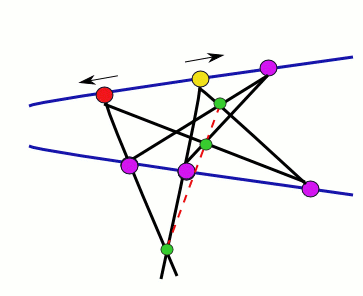
Pappus of Alexandria ( 290 – 350), one of the last great Greek mathematicians of Antiquity, proved that that given one set of points A, B, C on a line, and another set of points a, b, c on another line, then the intersection points X, Y, Z of line pairs Ab and aB, Ac and aC, Bc and bC are also on a Line. This line originates at the Vanishing Point.
Later Desargues (1591-1661) proved Pappus Theorem for Triangels. He proved that the three vertices of one triangle a, b, and c, and those of the other A, B, and C meet in a third point, and that these three points all lie on a common line called the Axis of Perspectivity.
Later Blaise Pascal (1623-1662) proved Pappus Theorem for Conics (Circles, Parabola, Hyperbola) in his ”Essay on Conics” (1640) when he was 16 years of Age.
About the Four Points of the Cross-Ratio
Finally 400 years later in 1803 Lazare Carnot found the answer to the Question of Leone Battista Alberti.
In his book “Géométrie de Position” he proved that the so called “Cross-Ratio” is always preserved in a Projection with One Point of View.
The Cross-Ratio is the Ratio of the Ratio of the Four Points A,B,C,D lying on a Line that intersects the Four Lines defined by a,b,c,d that orginate at the Vanishing Point O. Carnot proved that (AB)(CD)/(AC)(BD) = (A′B′)(C′D′)/(A′C′)(B′D′).
The Cross Ratio is not only the Cross-Ratio of the Four Points A,B,C,D. It is also the Cross-Ratio of the Four Lines and the Three Angles that originate out of the Vanishing Point. In this case (AB)(CD)/(AC)(BD)=Sin(AB) x Sin(CD)/Sin (AC) x Sin (BD).
This principle is called Duality. In 2D-Projective Geometry Connected Points and Lines, called an Incidence, are interchangeable.
There is a corresponding Duality in three-dimensional Projective Geometry between Points and Planes. Here, the line is its own Duality, because it is determined by either two points or two planes.
 Two examples: 2D: Two distinct Points determine a unique Line and two
distinct Lines determine a unique Point. 3-D: Three distinct Points
not all on the same Line determine a unique Plane and three distinct
Planes not all containing the same Line determine (meet in) a unique
Point.
Two examples: 2D: Two distinct Points determine a unique Line and two
distinct Lines determine a unique Point. 3-D: Three distinct Points
not all on the same Line determine a unique Plane and three distinct
Planes not all containing the same Line determine (meet in) a unique
Point.
The 24 Permutations of A,B,C and D produce 6 possible values of the Cross-Ratio, depending on the order in which the points are given. If k = 1, the other Cross-Ratio’s are 0 and infinity. This happens when point A = point D. In this case the Geometric Entity is an Equilateral Triangle.
If k = -1, the other Cross-Ratio’s are -1/2 and 2. This is called a Harmonic Cross-Ratio. This happens when the Internal Ratio of AC determinated by B is Equal to the External Ratio of AC determinated by D. When k=-1/2 and 2 the Geometric Entity is a Square.
If the Four Points of the Cross-Ratio are on a Line or a Circle, then the Cross Ratio is a Real Number, otherwise the Cross-Ratio is a Complex Number.
About the Four Layers of Geometry and the Four Points of the Cross-Ratio
In 1872 Felix Klein, published a new Mathematical Research Program called the Erlangen Program under the title Vergleichende Betrachtungen über neuere geometrische Forschungen.
In this program Projective Geometry was emphasized as the Unifying Frame for all other Geometries.
Although lines in the Projective Plane meet in one point of Infinity Klein argued that there could be two points of Infinity if the Projective Plane was a Surface Closed in Itself.
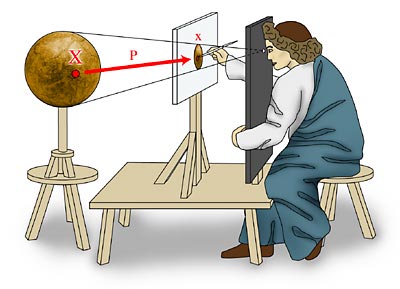
When we look at the Origin of Projective Geometry, the Artist painting A Sphere, Earth, on a Flat Surface, it is not difficult to realize that this Closed Surface is a Sphere.
.
Geometry is now divided into Four Layers. Each Layer adds a set of Assumptions that creates certain Invariants for that Layer.
An invariant is a property of a configuration of Geometric Entities that is not altered by any transformation belonging to the specific layer.
A transformation is an operation applied to a Geometric Entity. The most common transformations are Translation, Rotation and their Combinations (Reflection).
What we will see is that the Four Points of the Cross-Ratio are highly related to the Four Layers. In Every Higher Layer One Point of the Cross-Ratio is moved to the Internal Landscape, the Mind, of the Observer. This principle is called “As Within so Without“.
The First and most fundamental Layer is the Layer of Projective Geometry. This is the Layer of Human Perception and is invariant under the Cross-Ratio also called a Moebius Transformation.
The Second Layer is called Affine Geometry. In this layer Parallel Lines are preserved and the Assumption of a Plane at Infinity, the Horizon, is created. This Plane generates Parallel and Orthogonal Relationships between Geometric Entities by placing One of the Four Points of the Cross-Ratio in the Plane at Infinity.
Affine Geometry is Euclidean Geometry with congruence (something is the same when Shape and Size are the Same) and a metric (a definition of a Distance) left out. An affine transformation preserves straight lines and ratios of distances between points lying on a straight line.
This the layer of the Emotions, “the harmony of all parts in affinity to one another” of Leone Batista Alberti. In Affine Geometry the Frame of Reference of the Painter, the Floor, is created. On this Floor, the Horizon, the Plane at Infinity is drawn. From the Point of View of the Observer, it is not possible to Judge Distance or the-Sameness because a given Visual Object may be Large and Far away or Small and Close.
 The Third Layer, Metric Geometry, adds the concept of Distance
(Metric, Scale) to the Affine Layer. A Distance is a relation between
Two Points of the Cross-Ratio. This is the Layer of the Painter,
Creator, Observer, who creates his own Distance to the Distances he is
Painting in the External Frame he is looking at.
The Third Layer, Metric Geometry, adds the concept of Distance
(Metric, Scale) to the Affine Layer. A Distance is a relation between
Two Points of the Cross-Ratio. This is the Layer of the Painter,
Creator, Observer, who creates his own Distance to the Distances he is
Painting in the External Frame he is looking at.
Since Projective Space is the Space of Actual Perception, the true function of Metric Space is the Coordination of Various Perspectives. This is illustrated in Perspective Drawing, in which there are always Two Perspectives being Coordinated—the Vanishing Point and a Point just behind the Eyes of the Observer. Each of these is an instance of the One Point at Infinity.
The last, Fourth, Layer is the layer of Euclidian Geometry. In Euclidean Geometry Distance is Fixed (not Relative) and Scaled to a Unity (Meters). This leaves us with just One Point of the Cross-Ratio, the Unity, the One.
Between 1926 and his death in 1983 Alfred Tarski worked on the Axiomatization of Euclidean Geometry. In Tarski’s system there is only one type of Object: the One, The Point.
There are just two Geometrical notions between Points: the Ternary Relation of “in-Betweenness” and the Quaternary Relation of “Equidistance” or Congruence. Betweenness captures the Affine aspect of Euclidean Geometry; Equidistance/Congruence, its Metric aspect.
This is the Layer of the Human Expectation who has not Distanced Itself and is Looking Outside Through a Small Hole at the Future. The Expectation considers the Future as an Extension of the Past (Memory).
In Euclidian Geometry we have to Move Outside to the Objects to Measure their Distance and the Sameness with a Pre-Defined Unity.
If we don’t move to the Object we will measure an Illusion.
About Space measured by Time and Space measured by Space
At that Time Space was measured by Time.
The Physical System of the Megaliths was destroyed by the Great Flood of 3.117 BC but the Metric System survived thousands of years until the French Revolution.
On the 8th of May, 1790, Charles Maurice de Talleyrand at the end of the French Revolution, proposed before the National Assembly in Paris a Change to a Decimal Measurement System.
The Academy of Science recommended that the new definition for a Meter be equal to 1/10,000,000 of the distance between the North Pole and the Equator, and this was accepted by the National Assembly in 1791.
From that Time on Space was measured by Space.
Why the Future contains Infinite Possibilities
 A Painter or a Human always looks Forwards in Space. If there
are Parallel Lines visible they all Converge to a Vanishing Point at The
Horizon. The Horizon is a Parallel Line at Infinity.
A Painter or a Human always looks Forwards in Space. If there
are Parallel Lines visible they all Converge to a Vanishing Point at The
Horizon. The Horizon is a Parallel Line at Infinity.
We all know that the Parallel Line of the Horizon is caused by the fact that the Earth is a Moving Sphere. This Moving Sphere moves around other Spheres that move around other Spheres.
The Rotation of the Spheres in Space is used as a Clock. Every time when the Cycle of the Spheres repeats itself we add one unit to a standard Time-Measure. One Sun Cycle is named a Year. One Cycle of the Precession takes 25,920 Years.
We Measure our Time by the Cyclic Movement of Objects in Space. The Cyclic Movements caused by the Rotations of Objects around Objects (around Objects) is really a Rotating Rotating Rotation, a Spiraling Spiral.
We don’t live in the Sphere but we live and Move on the Surface of a Moving Sphere. That is why our Geometry is an Elliptic Geometry (or Projective Geometry).
Euclides and Pythagoras were aware of Projective Geometry (See also Pappus) but the Scientists of the Enlightenmentstarted to interpret their Theory with a Different Eye. They saw Numbers in a completely different way the Greek did.
The Scientist disconnected Number from Magnitude (Form) and created an Abstract Static Number Theory and an Abstract Static Theory of Physics. The Movement of our Universe, the Ether, came to a stilstand.
The Theory of Perspective Drawing, based on our Real Perception of Reality, is the same theory that generated Projective Geometry. We are now back to Normal again.
In the blog about Geometric Algebra I wrote about a very Independent Thinker called Dewey B. Larson.
He reinvented Physics and Projective Geometry in his own way, Calculated all the well known Physical Constants and based his Theory on a simple well know Assumption that Space and Time are Reciprocal (A Ratio of Ratio’s , the Cross-Ratio) because Velocity= dS(pace)/dT(ime).
Moving Movement is the Essence of our Reality.
What Larson calls “Motion” is the Ether Wind (or the Higgs Field) the Velocity which was measured in the North-South (Z) direction at 208 km/s in 1933 by Dayton C. Miller.
Einstein believed the results of the Michelson-Morley Experiments in 1887 that “proved” that the Moving Ether was non-existent. Now we know that the experiments were wrong. Einstein also did not believe that Space was Expanding. At this moment the Expanding Universe is confirmed by many observations.
When Space Expands, Time Compresses and fills up the Space to Keep Balance. Time Scales Space.
Space moves to Infinity. Time Moves to the Inverse of Infinity, Zero. Space is measured by the Linear Visible Scalar Number-System. Time is Measured with the Rotational Invisible Imaginary Number System.
Expanding Space is Linear Motion. Time is the Spiraling Motion of the Vortex.
Space is Yang and Time is Yin. Yin is feminine, Curved, Rotational, smooth or cold. Yang is masculine, Straight, Linear, rough or hot.
Space and Time are Complementary Duals that Move Around the Void.
If we look at the Human Perspective we now are able to understand what Time and Space Really are.
When we Look Forward we Experience Space. Time is always Behind our Back.
Human Senses and Conventional, Scientific Equipment can only Look Forward and therefore Measure Space (Distance) and the Change of Space (Velocity, Acceleration).
This is a Limitation of our Physical Sensory System, which evolved to measure Space, Scaled by Time, to produce what we Perceive as Causality–a Linear Ordering of Events.
Without the Cause-and-Effect System, the Sensory World of Space would just become Chaos.
Time, History, is Always Behind Us and Space, The Future, The Adjacent Possible, with Infinite Possibilities, is Always in Front of Us.
Let’s Move.
LINKS
About Pythagoras and Heliopolis (Egypt)
About Pythagoras
Paul Dirac: About Physics and Projective Geometry
About the Middle Ages
About Expanding Space and Not-Euclidian Geometry
About the Renaissance
About Resistance and Mass
About the Mathematics of Perspective
About the Ether
About Clean Space
About Projective Geometry
Pictures of the Projective Plane
About Geometric Algebra
About As Within, So Without
About the Reciprocal Theory of Dewey B. Larson
A Video about Mobius Transformations
About Projective Geometry and our Senses
About Projective Geometry and Geometric Algebra
About the Cube of Space
About Time and Paranormal Experiences
About Geometry
A Textbook about Metric Geometry
About the Four Points of View
About the Void
Why the Future is Open Space
About Alchemy and the Klein Bottle
About the Human Sensory System
Stuart Kaufmann: About the Adjacent Possible
Around 1400 during the Renaissance Painters started to look at Space with their own Eyes and discovered the Rules of Perspective Drawing.
Between 1600-1800 Perspective Theory changed from a Theory of Art to a Theory of Mathematics called Projective Geometry.
It took 400 Years before a few Mathematicians realized that Projective Geometry was the Foundation of Mathematics and it took another 100 years before Projective Geometry started to influence Physics.
In 1908 Hermann Minkowski discovered that Einstein’s Theory of Special Relativity could be analysed using Projective Geometry. Minkowski created a 4D Space-Time Metric Geometry in which he added one Time Dimension.
Many experiments now show that 4D-Space-Time is not sufficient to incorporate what Time Really is.
The essence of Our Universe is Movement, Expanding Space, and Movement = Space/Time (Space Divided By Time).
Both Time and Space are 3-Dimensional and represent a Different, Reciprocal, Complementary (Dual), View on Movement.
We can move independently in Time OR Space and in Time AND Space (The Chronotope).
The Future is Expanding Space with Infinite Potential.
Time moves behind Space and Scales Space.
About Perspective Drawing
A Mathematical Theory of Perspective Drawing could only be developed when the Renaissance freed painters to depict Nature in a way closer to what they Observed.
In the Middle Ages Social Status was very important. Important People or Buildings were always emphasized.
In the Renaissance the Artists started to look with their own Eyes and Created Pictures where the Viewer looked through the Eyes of the Painter.
The Florentine architect Filippo Brunelleschi (1337-1446) studied Greek Geometry, developed a theory of perspective and undertook painting just to apply his geometry.
The first treatise, Della pittura (1435) by Leone Battista Alberti (1404-72) furnished most of the rules.
Alberti regarded mathematics as the common ground of Art and the Sciences. “To make clear my exposition in writing this brief commentary on painting,” Alberti began his treatise Della pittura, “I will take first from the mathematicians those things which my subject is concerned”.
Alberti stressed that “all steps of learning should be sought from nature“. The ultimate aim of an artist is to imitate nature.

Perspective Machine designed by Albrecht Durer
The work of art is according to Alberti so constructed that it is impossible to take anything away from it or add anything to it, without impairing the beauty of the whole.
Beauty was for Alberti “the harmony of all parts in relation to one another,” and subsequently “this concord is realized in a particular number, proportion, and arrangement demanded by harmony“.
Alberti’s thoughts on harmony were not new – they could be traced back to Pythagoras – but he set them in a fresh context, which well fit in with the contemporary Aesthetic Discourse.
One of the earliest Artists to produce a book on how to draw in perspective was Albrecht Dürer. As well as discussing geometric methods, he also illustrated his book with a set of woodcuts showing practical tools for accurate perspective drawing. Other Artists like Leonardo Da Vinci developed comparable tools.
About Projective Geometry
Projective Geometry formalizes one of the Central Principles of Perspective Drawing and of Human Perception: Parallel Lines Meet at Infinity.

Parallel Lines meet at Infinity
In Projective Geometry one Never Measures Any Thing, instead, one Relates one Set of Points to another by a Line.
Alberti was the first to ask what two pictures have in common if two drawing screens are interposed between the viewer and the object, and the object is projected onto both resulting in two different pictures of the same scene.
The basic idea behind Linear Perspective is simple: in every painting an artist creates a “floor” or area of the painting where the figures and/or objects will be placed. The floor ends at a horizon line, and the horizon line has a Vanishing Point or Point of Convergence on it.
The artist then draws parallel lines radiating from the vanishing point outward. Images closest to the vanishing point should appear smaller and closer together, and images farthest from the vanishing point should appear larger and farther apart, giving the impression of depth and space in the painting.
Pappus of Alexandria ( 290 – 350), one of the last great Greek mathematicians of Antiquity, proved that that given one set of points A, B, C on a line, and another set of points a, b, c on another line, then the intersection points X, Y, Z of line pairs Ab and aB, Ac and aC, Bc and bC are also on a Line. This line originates at the Vanishing Point.
Later Desargues (1591-1661) proved Pappus Theorem for Triangels. He proved that the three vertices of one triangle a, b, and c, and those of the other A, B, and C meet in a third point, and that these three points all lie on a common line called the Axis of Perspectivity.
Later Blaise Pascal (1623-1662) proved Pappus Theorem for Conics (Circles, Parabola, Hyperbola) in his ”Essay on Conics” (1640) when he was 16 years of Age.
About the Four Points of the Cross-Ratio
Finally 400 years later in 1803 Lazare Carnot found the answer to the Question of Leone Battista Alberti.
In his book “Géométrie de Position” he proved that the so called “Cross-Ratio” is always preserved in a Projection with One Point of View.
The Cross-Ratio is the Ratio of the Ratio of the Four Points A,B,C,D lying on a Line that intersects the Four Lines defined by a,b,c,d that orginate at the Vanishing Point O. Carnot proved that (AB)(CD)/(AC)(BD) = (A′B′)(C′D′)/(A′C′)(B′D′).
The Cross Ratio is not only the Cross-Ratio of the Four Points A,B,C,D. It is also the Cross-Ratio of the Four Lines and the Three Angles that originate out of the Vanishing Point. In this case (AB)(CD)/(AC)(BD)=Sin(AB) x Sin(CD)/Sin (AC) x Sin (BD).
This principle is called Duality. In 2D-Projective Geometry Connected Points and Lines, called an Incidence, are interchangeable.
There is a corresponding Duality in three-dimensional Projective Geometry between Points and Planes. Here, the line is its own Duality, because it is determined by either two points or two planes.

The
Cross-Ratio k is dependent on the Order of the Four Points. It
converges to 0 and infinity when k=1 and to -1/2 and 2 when k= -1.
The 24 Permutations of A,B,C and D produce 6 possible values of the Cross-Ratio, depending on the order in which the points are given. If k = 1, the other Cross-Ratio’s are 0 and infinity. This happens when point A = point D. In this case the Geometric Entity is an Equilateral Triangle.
If k = -1, the other Cross-Ratio’s are -1/2 and 2. This is called a Harmonic Cross-Ratio. This happens when the Internal Ratio of AC determinated by B is Equal to the External Ratio of AC determinated by D. When k=-1/2 and 2 the Geometric Entity is a Square.
If the Four Points of the Cross-Ratio are on a Line or a Circle, then the Cross Ratio is a Real Number, otherwise the Cross-Ratio is a Complex Number.
About the Four Layers of Geometry and the Four Points of the Cross-Ratio
In 1872 Felix Klein, published a new Mathematical Research Program called the Erlangen Program under the title Vergleichende Betrachtungen über neuere geometrische Forschungen.
In this program Projective Geometry was emphasized as the Unifying Frame for all other Geometries.
Although lines in the Projective Plane meet in one point of Infinity Klein argued that there could be two points of Infinity if the Projective Plane was a Surface Closed in Itself.
When we look at the Origin of Projective Geometry, the Artist painting A Sphere, Earth, on a Flat Surface, it is not difficult to realize that this Closed Surface is a Sphere.
.
Geometry is now divided into Four Layers. Each Layer adds a set of Assumptions that creates certain Invariants for that Layer.
An invariant is a property of a configuration of Geometric Entities that is not altered by any transformation belonging to the specific layer.
A transformation is an operation applied to a Geometric Entity. The most common transformations are Translation, Rotation and their Combinations (Reflection).
What we will see is that the Four Points of the Cross-Ratio are highly related to the Four Layers. In Every Higher Layer One Point of the Cross-Ratio is moved to the Internal Landscape, the Mind, of the Observer. This principle is called “As Within so Without“.
The First and most fundamental Layer is the Layer of Projective Geometry. This is the Layer of Human Perception and is invariant under the Cross-Ratio also called a Moebius Transformation.
The Second Layer is called Affine Geometry. In this layer Parallel Lines are preserved and the Assumption of a Plane at Infinity, the Horizon, is created. This Plane generates Parallel and Orthogonal Relationships between Geometric Entities by placing One of the Four Points of the Cross-Ratio in the Plane at Infinity.
Affine Geometry is Euclidean Geometry with congruence (something is the same when Shape and Size are the Same) and a metric (a definition of a Distance) left out. An affine transformation preserves straight lines and ratios of distances between points lying on a straight line.
This the layer of the Emotions, “the harmony of all parts in affinity to one another” of Leone Batista Alberti. In Affine Geometry the Frame of Reference of the Painter, the Floor, is created. On this Floor, the Horizon, the Plane at Infinity is drawn. From the Point of View of the Observer, it is not possible to Judge Distance or the-Sameness because a given Visual Object may be Large and Far away or Small and Close.

In Eucludian Geometry A Ruler contains a Fixed Scale
Since Projective Space is the Space of Actual Perception, the true function of Metric Space is the Coordination of Various Perspectives. This is illustrated in Perspective Drawing, in which there are always Two Perspectives being Coordinated—the Vanishing Point and a Point just behind the Eyes of the Observer. Each of these is an instance of the One Point at Infinity.
The last, Fourth, Layer is the layer of Euclidian Geometry. In Euclidean Geometry Distance is Fixed (not Relative) and Scaled to a Unity (Meters). This leaves us with just One Point of the Cross-Ratio, the Unity, the One.
Between 1926 and his death in 1983 Alfred Tarski worked on the Axiomatization of Euclidean Geometry. In Tarski’s system there is only one type of Object: the One, The Point.
There are just two Geometrical notions between Points: the Ternary Relation of “in-Betweenness” and the Quaternary Relation of “Equidistance” or Congruence. Betweenness captures the Affine aspect of Euclidean Geometry; Equidistance/Congruence, its Metric aspect.
This is the Layer of the Human Expectation who has not Distanced Itself and is Looking Outside Through a Small Hole at the Future. The Expectation considers the Future as an Extension of the Past (Memory).
In Euclidian Geometry we have to Move Outside to the Objects to Measure their Distance and the Sameness with a Pre-Defined Unity.
If we don’t move to the Object we will measure an Illusion.
About Space measured by Time and Space measured by Space
The
Ancient Sumerians knew that the Length of one side of a Hexagon is the
same length as is the Radius of the Circle that circumscribes this
Hexagon (See Pascals Theorem).
They
also knew that the Stars of the Constellations of the Zodiac shift
Counterclockwise, at the rate of 72 years/degree, because of the
Precession of the Earth’s axis. One Wobble takes 25.920 years.
The
length of one side of the Earth Hexagon is therefore the Distance
traveled by the Constellations of the Zodiac along the horizon during
25.920/6=4,320 years.
They then subdivided this distance by 7,200 which produced the Royal Mile that was subdivided into 1,760 Royal Cubits.
Before 3.117 BC the complete Earth was covered with a uniform Geodesic System that was based on the Rotation and Precession of the Constellations of the Zodiac. This System was implemented in the Megaliths.At that Time Space was measured by Time.
The Physical System of the Megaliths was destroyed by the Great Flood of 3.117 BC but the Metric System survived thousands of years until the French Revolution.
On the 8th of May, 1790, Charles Maurice de Talleyrand at the end of the French Revolution, proposed before the National Assembly in Paris a Change to a Decimal Measurement System.
The Academy of Science recommended that the new definition for a Meter be equal to 1/10,000,000 of the distance between the North Pole and the Equator, and this was accepted by the National Assembly in 1791.
From that Time on Space was measured by Space.
Why the Future contains Infinite Possibilities

We all know that the Parallel Line of the Horizon is caused by the fact that the Earth is a Moving Sphere. This Moving Sphere moves around other Spheres that move around other Spheres.
The Rotation of the Spheres in Space is used as a Clock. Every time when the Cycle of the Spheres repeats itself we add one unit to a standard Time-Measure. One Sun Cycle is named a Year. One Cycle of the Precession takes 25,920 Years.
We Measure our Time by the Cyclic Movement of Objects in Space. The Cyclic Movements caused by the Rotations of Objects around Objects (around Objects) is really a Rotating Rotating Rotation, a Spiraling Spiral.
We don’t live in the Sphere but we live and Move on the Surface of a Moving Sphere. That is why our Geometry is an Elliptic Geometry (or Projective Geometry).
Euclides and Pythagoras were aware of Projective Geometry (See also Pappus) but the Scientists of the Enlightenmentstarted to interpret their Theory with a Different Eye. They saw Numbers in a completely different way the Greek did.
The Scientist disconnected Number from Magnitude (Form) and created an Abstract Static Number Theory and an Abstract Static Theory of Physics. The Movement of our Universe, the Ether, came to a stilstand.
The Theory of Perspective Drawing, based on our Real Perception of Reality, is the same theory that generated Projective Geometry. We are now back to Normal again.
In the blog about Geometric Algebra I wrote about a very Independent Thinker called Dewey B. Larson.
He reinvented Physics and Projective Geometry in his own way, Calculated all the well known Physical Constants and based his Theory on a simple well know Assumption that Space and Time are Reciprocal (A Ratio of Ratio’s , the Cross-Ratio) because Velocity= dS(pace)/dT(ime).
Moving Movement is the Essence of our Reality.
What Larson calls “Motion” is the Ether Wind (or the Higgs Field) the Velocity which was measured in the North-South (Z) direction at 208 km/s in 1933 by Dayton C. Miller.
Einstein believed the results of the Michelson-Morley Experiments in 1887 that “proved” that the Moving Ether was non-existent. Now we know that the experiments were wrong. Einstein also did not believe that Space was Expanding. At this moment the Expanding Universe is confirmed by many observations.
When Space Expands, Time Compresses and fills up the Space to Keep Balance. Time Scales Space.
Space moves to Infinity. Time Moves to the Inverse of Infinity, Zero. Space is measured by the Linear Visible Scalar Number-System. Time is Measured with the Rotational Invisible Imaginary Number System.
Expanding Space is Linear Motion. Time is the Spiraling Motion of the Vortex.
Space is Yang and Time is Yin. Yin is feminine, Curved, Rotational, smooth or cold. Yang is masculine, Straight, Linear, rough or hot.
Space and Time are Complementary Duals that Move Around the Void.
If we look at the Human Perspective we now are able to understand what Time and Space Really are.
When we Look Forward we Experience Space. Time is always Behind our Back.
Human Senses and Conventional, Scientific Equipment can only Look Forward and therefore Measure Space (Distance) and the Change of Space (Velocity, Acceleration).
This is a Limitation of our Physical Sensory System, which evolved to measure Space, Scaled by Time, to produce what we Perceive as Causality–a Linear Ordering of Events.
Without the Cause-and-Effect System, the Sensory World of Space would just become Chaos.
Time, History, is Always Behind Us and Space, The Future, The Adjacent Possible, with Infinite Possibilities, is Always in Front of Us.
Let’s Move.
LINKS
About Pythagoras and Heliopolis (Egypt)
About Pythagoras
Paul Dirac: About Physics and Projective Geometry
About the Middle Ages
About Expanding Space and Not-Euclidian Geometry
About the Renaissance
About Resistance and Mass
About the Mathematics of Perspective
About the Ether
About Clean Space
About Projective Geometry
Pictures of the Projective Plane
About Geometric Algebra
About As Within, So Without
About the Reciprocal Theory of Dewey B. Larson
A Video about Mobius Transformations
About Projective Geometry and our Senses
About Projective Geometry and Geometric Algebra
About the Cube of Space
About Time and Paranormal Experiences
About Geometry
A Textbook about Metric Geometry
About the Four Points of View
About the Void
Why the Future is Open Space
About Alchemy and the Klein Bottle
About the Human Sensory System
Stuart Kaufmann: About the Adjacent Possible
About Number and Magnitude
Monday, January 9th, 2012
A few years ago a Revolution in Mathematics and Physics has started. This revolution is caused by Geometric Algebra.
In Geometric Algebra the Ancient Theories of Euclid and Pythagoras are reevaluated.
Numbers are Scalar (Quantum) Movements of Geometric Patterns and not Static Symbols of Abstractions that have nothing to do with our Reality.
Movements and not Forces are the Essence of Physics.
The basic rule Movement = Space/Time (v=s/t) shows that Time and Space are two Reciprocal 3D-Spaces. Our Senses Experience Space and not Time.
The Simple Rule N/N=1/1=1 balances the Duals of Space and Time. One Unit Step in Space is always Compensated by One Unit Step in Time.
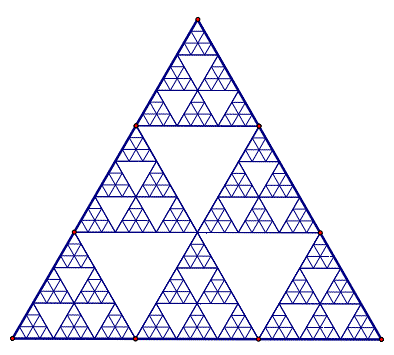
Geometric Algebra has a strange relationship with Pascals Triangle. This Triangle, also called the Binomial Expansion, contains all the Possible Combinations of two Independent Variables. Our Universe is a Combination of Combinations exploring Every Possibility.
The last and perhaps most important Discovery in Mathematics called Bott Periodicity shows itself in Pascals Triangle.
Bott Periodicity proves that we live in a Cyclic Fractal Universe, the Wheel of Fortune, that is Rotating around the Void, the Empty Set. The Empty Set contains Every Thing that is Impossible in our Universe.
This blog is not a Scientific Article. I have tried to connect the Old Sciences and the New Sciences in my own Way.
It contains many links to Scientific Articles and even Courses in Geometric Algebra.
So if you want to Dig Deeper Nothing will Stop You.
About the One and the Dirac Delta Function
Every Thing was created out of No Thing, the Empty Set, ɸ, the Void, the Tao. The Empty Set contains 0 objects.
The Empty Set is not Empty. It contains Infinite (∞) Possibilities that are Impossible.
Every impossibility has a probability of 0 but the sum of all possibilities (1/∞=0) is always 1. In the beginning ∞/∞ =1 or ∞x0=1.
This relationship is represented by the Dirac Delta Function. It is used to simulate a Point Source of Energy (a Spike, an Explosion) in Physics.
The Delta is reprented by the Symbol Δ, a Triangle. The Delta is called Dalet in the Phoenican and Hebrew Alphabet. Daleth is the number 4 and means Door.
The original symbol of the Delta/Daleth contains two lines with a 90 Degree Angle. Two orthogonal lines create a Square or Plane.
The Dirac Delta Function is defined as a Square with an Area of 1, a Width of 1/n and a Height of n where n->∞.
The Dirac Delta Function is a Line with an Area of 1.
In the Beginning a Huge Explosion took place that created the Universe.
The Dirac Delta Function δ (x) has interesting properties: δ (x) = δ (-x), δ (x) = δ (1/x). It has two Symmetries related to the Negative Numbers and the Rational Numbers.
When we move from 2D to 1D, the Number Line, the Delta Function becomes the Set of the Numbers N/N =1.

The Tetraktys of Pythagoras
Creation is an Expansion of the 1/1 into the N/N, adding 1/1 all the time, until ∞/∞ is reached. At that moment every Impossibility has been realized.
To move Back to the Void and restore the Eternal Balance of the One, Dividing (Compression) has to be compensated by Multiplication (Expansion).
At the End of Time N/M and M/N have to find Balance in the N/N, move Back to 1/1, Unite in the 0 and become The Void (ɸ) again.
About the Strange Behavior of Numbers
The big problem of the Numbers is that they sometimes behave very differently from what we Expect them to do.
This Strange Behavior happens when we try to Reverse what we are doing.
It looks like the Expansion of the Universe of Numbers is Easy but the Contraction creates many Obstacles.
It all starts with the Natural Numbers (1,2,3,).
When we Reverse an Addition (Subtract) and move over the Line of the Void Negative Numbers appear. Together with the Natural Numbers they are called the Integers.
The same happens when we Reverse a Division and the Fractions (the Rational Numbers) (1/3, 7/9) suddenly pop up.
An Integer N is a Rational Number divided by 1 (N/1).
The Integers are the Multiples of 1, the Fractions are its Parts.
Numbers behave even stranger when we want to Reverse a Repeating Repeating Addition (Irrational Numbers) and want to calculate a Rational Power (2**1/2).
The Complex Numbers (or Imaginary Numbers), based on the Square Root of -1 called i, are a combination of the Negative Numbers and the Irrational Numbers.
Irrational Numbers ( the Pythagorean Theorem), Fractions (a Piece of the Cake) and Negative Numbers (a Debt) are part of our Reality but the Strange Number i represents something we cannot Imagine.
About the Duality and the Expansion of Space
In the beginning the only One who was in existence was the 1.
When the One divide itself again the number -1, the Complement of 1, came into existence.
1 and -1 are voided in the No Thing, the Empty Set, 0: -1 + 1 = 0.
The Two, the Duality, both started to Expand in Two Opposite Directions (<– and +->) both meeting in the ∞/∞. This expansion is what we call Space.
Space is a Combination of the Strings S(1,1,1,1,1,…) and -S = (-1,-,1,-,1,-1,…) where S+S=(0,0,0,0,0,0,…).
The Expansion pattern of Space is a Recursive Function S: S(N)=S(N-1)+1 in which + means concatenate (or add) the String “,1″.
An Addition X + Y is a concatenation of S(X) and S(Y). A Substraction X-Y is a concatenation of S(X) and -S(Y). In the last case all the corresponding combinations of 1 and -1 are voided. (1,1,1,1)-(1,1,1)=(0,0,0,1)=(1).
Multiplication XxY is Adding String S(Y) every time a “1″ of S(X ) is encountered: 111 x 11 = 11 11 11. Dividing X/Y is Subtracting S(X) every time a “1″ of S(Y) is encountered:.111 111 1/111=11 1/111. In the last example a Fraction 1/111 appears.
This Number System is called the Unary Number System.
About the Trinity and the Compression of Space called Time
The Strange Behavior of Numbers is caused by the Limitations of our Memory System. We are unable to remember long strings that contain the same Number.
To make things easy for us we Divide Space into small Parts so we were able to Re-Member (Re-Combine the Parts).
When we want to Re-member, Move Back in Time, we have to Compress Expanding Space.
Compressed Space is Time.
Time and Space have a Reciprocal Relationship called Movement (Velocity = Space/Time).
There are many ways ( (1,1,1), (1,1,1),..) or ((1,1),(1,1))) to Compress a String in Repeating Sub-Patterns.
In the blog About the Trinity I showed that the most Efficient Way to group the One’s is to make use of a Fractal Pattern (a Self Reference) and Groups of Three Ones.
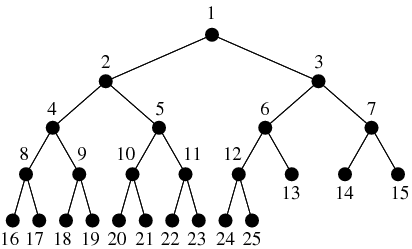
The Trinity applied to the Trinity ( A Fractal) is a Rotating Binary Tree. Binary Trees represent the Choices we make in Life.
The rotating Expanding Binary Trees generate the Platonic Solids (see linked video!) when the (number)-parts of the Binary Tree Connect.
When we connect Three Ones (1,1,1) by Three Lines (1-1,1-1,1-1) a 2 Dimensional Triangle Δ is Created.
If we take the Δ as a new Unity we are able to rewrite the patterns of 1′s and -1′s into a much Shorter Pattern of Δ’s and 1′s: (1,1,1),(1,1,1),(1,1,1), 1,1 becomes Δ,Δ,Δ,1,1.
We can repeat this approach when there is still a Trinity left: Δ,Δ,Δ,1,1 becomes ΔxΔ,1,1.
This Number System is called the Ternary Number System.
About Ratio’s and Magnitudes
According to Euclid “A Ratio is a sort of relation in respect of size between two magnitudes of the same kind“.
A Magnitude is a Size: a property by which it can be compared as Larger or Smaller than other objects of the Same Kind. A Line has a Length, a Plane has an Area (Length x Width), a Solid a Volume (Length xWitdth x Height).
For the Greeks, the Numbers (Arithmoi) were the Positive Integers. The objects of Geometry: Points, Lines, Planes , were referred to as “Magnitudes” (Forms). They were not numbers, and had no numbers attached.
Ratio, was a Relationship between Forms and a Proportion was a relationship between the Part and the Whole (the Monad) of a Form.
Newton turned the Greek conception of Number completely on its head: “By Number we understand, not so much a Multitude of Unities, as the abstracted Ratio of any Quantity, to another Quantity of the same Kind, which we take for Unity”.
We now think of a Ratio as a Number obtained from other numbers by Division. A Proportion, for us, is a statement of equality between two “Ratio‐Numbers”.
This was not the thought pattern of the ancient Greeks. When Euclid states that the ratio of A to B is the same as the ratio of C to D, the letters A, B, C and D do not refer to numbers at all, but to segments or polygonal regions or some such magnitudes.
The Ratio of two geometric structures was determinated by fitting the Unit Parts of the first geometric Stucture into the Other.
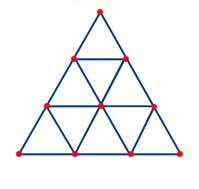
The Perfect Triangle of the Tetraktys contains 9 = 3x3 Triangels. A Triangle contains 3 Lines and 3 Points.
The Mathematics of Euclid is not a Mathematics of Numbers, but a Mathematics of Forms.
The symbols, relationships and manipulations have Physical or Geometric Objects as their referents.
You cannot work on this Mathematics without Knowing (and Seeing) the Objects that you are Working with.
About Hermann Grassman, David Hestenes and the Moving Line called Vector
Hermann Grasmann lived between 1809 and and 1877 in Stettin (Germany). Grassmann was a genius and invented Geometric Algebra a 100 years before it was invented.
In his time the most important mathematicians did not understand what he was talking about although many of them copied parts of his ideas and created their own restricted version. None of them saw the whole Grassmann was seeing.
When he was convinced nobody would believe him he became a linguist. He wrote books on German grammar, collected folk songs, and learned Sanskrit. His dictionary and his translation of the Rigveda were recognized among philologists.
Grassmann took over the heritage of Euclid and added, Motion, something Euclid was aware of but could not handle properly.
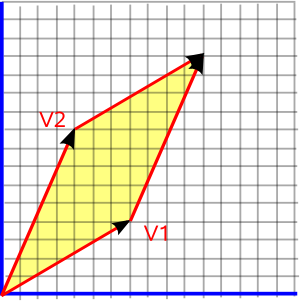
Grassmann became aware of the fact your hand is moving when you draw a 2D Geometric Structure. He called the Moving Lines, that connect the Points, Displacements (“Strecke”).
In our current terminology we would call the Displacements “Vectors”.
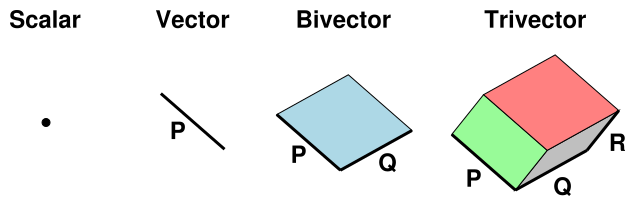
Vector algebra is simpler, but specific to Euclidean 3-space, while Geometric Algebra works in all dimensions. In this case Vectors become Bi/Tri or Multi-Vectors (Blades).
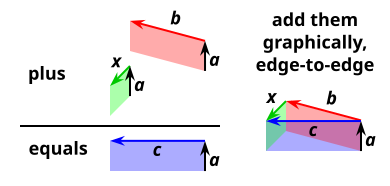
The Trick of Grassmann was that he could transform every transformation on any geometrical structure into a very simple Algebra. Multi-Dimensional Geometric Structures could be Added, Multiplied and Divided.
The Greek Theory of Ratio and Proportion is now incorporated in the properties of Scalar and Vector multiplication.
About a 100 years later David Hestenes improved the Theory of Grassmann by incorporating the Imaginary Numbers. In this way he united many until now highly disconnected fields of Mathematics that were created by the many mathematicians who copied parts of Grassmanns Heritage.
About Complex Numbers, Octions, Quaternions, Clifford Algebra and Rotations in Infinite Space
Grassmann did not pay much attention to the Complex Numbers until he heard of a young mathematician called William Kingdon Clifford (1845-1879).
Complex numbers are ,just like the Rationals (a/b), 2D-Numbers. A Complex number Z = a + ib where i**2=-1. Complex Numbers can be represented in Polar Coordinates: Z = R (cos(x) + i sin(x)) where R = SQRT(a**2 + b**2). R is the Radius, the Distance to the Center (0,0).
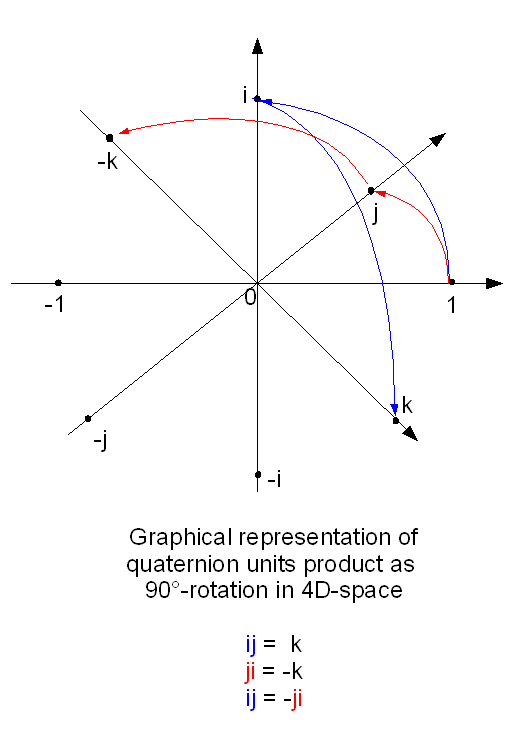
When you have defined a 2D-complex Number it is easy to define a 4-D-Complex Number called a Quaternion: Z = a + ib + jc + kd or a 8-D Complex Number called an Octonion.
William Rowan Hamilton, the inventor of the Quaternions, had big problems to find an interpretation of all the combinations i, j and k until he realized that i**2 =j**2 = k**2 = ijk=-1.
What Hamilton did not realize at that time was that he just like Grassmann had invented Vector Algebra and Geometric Algebra.
This all changed when William Kingdon Clifford united everything in his new Algebra. Clifford’s algebra is composed of elements which are Combinations of Grassman’s Multivectors.
The Clifford Algebra that represents 3D Euclidean Geometry has 8 = 2**3 components instead of 3: 1 number (Point), 3 vectors (Length), 3 bivectors (Area) and 1 trivector (Volume).
It turns out if you use combinations of these elements to describe your geometric objects you can do the same things you did before (you still have 3 vector components).
In addition, you can have additional data in those other components that let you find distances and intersections (and a lot of other useful information) using simple and (computationally) cheap numerical operations.
The most important Insight of William Kingdom Clifford was that the Complex Numbers are not Numbers all.
They are Rotations in higher Dimensional Spaces.
About Pascal’s Triangle and Mount Meru
The String 1,3,3,1 of Clifford’s 3D Geometry is related to the 4th Level of Pascal’s Triangle. Level N of Pascal’s Triangle represents N-1-Dimensional Geometries.
The Sum of every level N of the Triangle is 2**N. This Number expresses the Number of Directions of the Geometric Structure of a Space with Dimension N.
A Point has 0 Direction, while a Line has 2 Directions, relative to its Center point, a Plane has 4 Directions, relative to its Center Point, and a Cube has 8 directions, relative to its Center point.
Pascal’s Triangle is also called the Binomial Expansion. This Expansion shows all the Combinations of two letters A and B in the function (A+B)**N. Level 1 of the Triangle is (A+B)**0 = 1 and level 2 is A x A + 2 A x B + B x B -> 1,2,1.
The Binomial Expansion converges to the Bell-Shaped Normal Distribution when N-> ∞.
The Diagonals of Pascal’s Triangle contain the Geometric Number Systems (Triangular Numbers, Pyramid Numbers, Pentatonal Numbers, ..) and the Golden Spiral of the Fibonacci Numbers.
Pascal’s Triangle is a Repository of all the Possible Magnitudes and their Components.
The Normal Distribution shows that the first level of the Triangle (the Tetraktys) is much more probable than the last levels.

The Hexagonal Numbers
The Tetraktys is an Ancient Vedic Mathematical Structure called the Sri Yantra, Meru Prastara or Mount Meru.
About Numbers, Operations and the Klein Bottle
The Complex Numbers are not “Numbers” (Scalars) at all.
They are “Operations” (Movements) that can be applied to Magnitudes (Geometries) and Magnitudes are Combinations of the Simple Building Blocks of the Tetraktys, Points and Lines.
The Tao of Ancient China was not for nothing represented by a Flow of Water. According to the Ancient Chinese Mathematicians Every Thing Moves. In the Beginning there was only Movement.
In the Beginning only the One was Moved but when the Duality was created the Two moved around each other never getting into contact to Avoid the Void.
When we look at the Numbers we now can see that they are the result of the Movements of the first Diagonal of Pascals Triangle, the 1′s (Points) or better the Powers of the One: 1 **N (where N is a Dimension).
Even in the most simple Number System, the Unary Number System, Concatenation is an Operation, An Algorithm.
The Mathematician John Conway recently invented a new Number System called the Surreal Numbers that contains Every Number you can Imagine.
The Surreal Numbers are created out of the Void (ɸ) by a simple Algorithm (Conway calls an Algorithm a Game) that describes Movements (Choices of Direction: Up, Down, Left, Right, ..) that help you to Navigate in the N-Dimensional Number Space.
The Ancient Chinese Mathematicians played the same Game with the Numbers.
Algorithms were already known for a very long time by the Ancient Vedic Mathematicians. They called them Yantra’s.
Geometry is concerned with the Static Forms of Lines and Points but there are many other more “Curved” forms that are the result of Rotating Expansion and Compression. These forms are researched by the modern version of Geometry called Topology.
The most interesting 4D Topological Structure is the Klein Bottle. The Klein Bottle is a combination of two Moebius Rings. It represents a Structure that is Closed in Itself.
It can be constructed by gluing both pairs of opposite edges of a Rectangle together giving one pair a Half-Twist. The Klein Bottle is highly related to the Ancient Art of Alchemy.
The movement of the Duality around the Void can be represented by a Moebius Ring the Symbol of Infinity ∞.
Later in this Blog we will see why the Number 8 is a Rotation of ∞ and the symbol of Number 8 is a combination of the symbol of the number 3 and its mirror.
First we will have a look at the Reciprocal Relation between Space and Time.






























0 comments:
Post a Comment